Hex-Editing Guide by Vaskéz
Intro (for beginners)
Hex-editing, also called hexing is short for hexadecimal editing. It is so called because hex-editors display the data in a file in terms of hexadecimal numbers. What is the point in hexing? Well, it allows you to change any file almost in any way you wish. The drawback is that all you see is a bunch of numbers and letters so first you have to work out what each position in the file and the value in that position, represents.
The position of a value in the file is known as the offset because its address is the number by which it is offset from the first position in the file. The first position always has an offset of 0 because it IS the start of the file so it is not offset from the start at all. And so the 3rd value is at offset 2 (remember we start counting at 0).
The hexadecimal number system
A hex-editor displays the bits (binary digits, 1s and 0s) of a file in terms of hexadecimal numbers, as already mentioned. The reason for this is that even a relatively small number written in binary notation takes a lot of space to write. Hexadecimal (from now on referred to as hex) notation saves a lot of space when it comes to displaying the number because each hex digit represents 4 binary digits. I’ll explain why later.
For those who don’t know how the hex number system works I will explain here.
First of all it is important to know that there are 2 ways of indicating that a number is written in hex notation. You can use ‘0x’ at the beginning of the number or an ‘H’ (or ‘h’) at the end. For example:
0x8
and
8H
both represent a decimal 8 in hex notation. In case you don’t know, decimal is the ‘normal’ number system we use, with the digits 0,1,2,3,4,5,6,7,8,9. So called because deci means ten and the decimal number system has ten different digits.
Similarly, the hexadecimal number system is so called because it has 16 different digits:
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F, where A=10 (in decimal), B=11, C=12, D=13, E=14 and F=15.
To understand how to convert from decimal to hex and vice-versa, it is better to think about the way the decimal system works, first.
In decimal, each position in the number is worth ten times the one to its right. Therefore ten is known as the base of the decimal number system. Similarly, sixteen is the base of the hexadecimal number system, because each position is worth sixteen times the one to its right. This is true for any number system: as you move right to left, each position is worth the base of the number system times the position to its right. In binary, the base is 2 and each position is worth 2 times the one to its right.
To get the final value of a number in any number system you multiply the value in the position with the value of the position and add all the values up. For example:
Take, in decimal: 1111 (one thousand one hundred and eleven). The right-most position is worth 1 because it is 10 to the power of 0 (100). The second position is worth 10 which is 101 and the third from the right is worth 100 (102), while the last position is worth 1000 (103). And each position is multiplied by the value in the position to give the number. 1111 is equal to 1*100 + 1*101 + 1*102 + 1 *103 which equals 1 + 10 + 100 + 1000 = 1111. Simple as that. Except we don’t normally think about it in so much detail.
Similarly, 1234 is 4*100 + 3*101 + 2*102 + 1 *103 which equals 4 + 30 + 200 + 1000 = 1234 (one thousand two hundred and thirty-four).
The general rule is: Each position is worth the base of the number system, raised to the power of its number in the sequence counting along from the right, starting at 0. In decimal the position of the ‘3’ in 3000000 is worth 106 because the base is 10 and the position of the 3 from the right is 6 because we start counting at 0.
The reason I went through all that is to make it easy to understand the hexadecimal system. Remember the general rules, each position is worth the base times the number of the position counting from the right, starting at 0 and the value of the number overall is the sum of the values in each position multiplied by the value of the position. So in hexadecimal:
0x1111 is worth (starting on the right remember):
1*160 + 1*161 + 1*162 + 1*163 which equals 1 + 16 + 256 + 4096 = 4369 (in decimal, in general, when there is no symbol next to the number, it is in decimal notation).
One more example, using the ‘extra’ digits in hex:
0xABCD is worth:
13*160 + 12*161 + 11*162 + 10*163 = 13 + 192 + 2816 + 40960 = 43981.
As you can see, even against decimal, we save one digit because the number 43981 is given by 5 digits but its equivalent, 0xABCD is only 4 digits.
Now, as I said, hex notation is used to display the 1s and 0s of a file. In binary, the number 43981 would be 1010101111001101B (B means binary, not to be confused with the B in hex notation which means 11, hehe). As you can see this takes up 16 digits as opposed to the 4 used in the hex notation. The reason for this is that 24 = 16. The base of the binary system is 2 and the base of the hex system is 16. So hex saves space.
The Hex-Editor Display
The basic function of most hex-editors is the same. On the left are the hex offsets of the start of each row of 16 bytes. In the middle is the big block of hexadecimal values representing the file. The values are in pairs as you should be able to see. This is because (it is common knowledge) that there are 8 bits in a byte. And remember, each hex digit represents 4 bits (binary digits). Therefore 2 hex digits represent 8 bits, in other words, 1 byte. So the hex numbers are displayed as single bytes in a hex editor, for convenience. The offset is also measured as the number of bytes up to that point. For example, at offset 0x20, you will find the 33rd byte (remember, start at 0) because 0x20 equals 32 in decimal.
On the right of the display, you should find a section where there are actually readable strings. This section is like a text-editor. You may have heard of the ASCII table, which shows the decimal and hexadecimal codes for each character on the keyboard. On the right, you will find the ASCII character representation for each byte in the file. One byte represents one character. Of course, often, the characters will be meaningless because the data in that position is not meant to be text data. However, if you can read it, it is most likely to be text data. Most hex-editors let you type normally in this text section and will automatically insert the hex values corresponding to the characters you typed in, in the hex section. Of course, if you have an ASCII table handy you could type the hexadecimal number into the hex area and watch the characters appear (if you are crazy and have nothing better to do).
Hex-Editing the Infinity Engine Files
Having read the previous section, you will understood that references to file names such as in the “resource key” for a spell effect, will be readable as normal text in a hex editor, and you can edit them just as easily as if you were using IEEP. Of course numbers must be converted to hexadecimal (use a calculator for big numbers) and entered in the hex section in the editor. DO NOT try and type decimal numbers into the text area using your numpad because this will just enter the ASCII code for the number characters into the hex area.
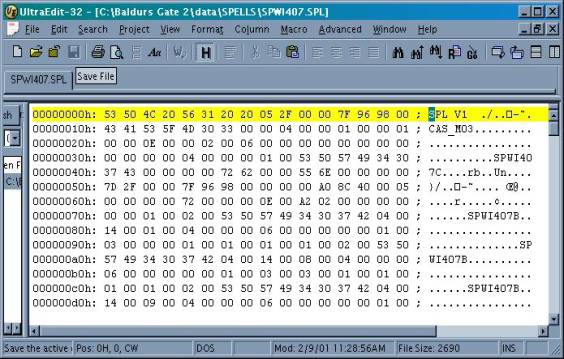
As you can see from the above picture, the hex offset at the start of each column is shown on the left. The main hexing area is in the middle and the ASCII text area is on the right. The file being edited here is the .spl file for the wizard spell “Monster Summoning II” from BG2. As you can see, at offset 00000010h (10h), there is the reference for the spell completion sound. You can see the values 43 41 53 5F 4D 30 33 00 which represent the ASCII characters CAS_M03, shown on the left. You can also type in those characters if you click on the text area and the hex values will appear.
One thing to note for hex-editing IE files: The general rule for ANY number system is that the least significant digit (worth the least) is always on the right, as I have shown in earlier sections. However, the numbers in IE files seem to be written in little-endian format which means that the least significant digit is written in the lowest address (offset). Which means that the number 43981 would not be written AB CD, rather, CD AB. The values retain their order within the bytes but the actual order of the bytes is swapped around. This complicates things a little but if you remember this it shouldn’t be too much of a problem. This is most useful to know when you want your item or spell or creature to have the same name as an existing thing in the game but you don’t want to create a whole new entry in the dialog.tlk file. In this case, you can hex-edit the file and enter in the string reference number to the text that you want. This will be entered in little-endian format as shown above. I have not investigated this thoroughly, but it seems to be the case wherever I have looked.
As an example, let’s say that you want your spell to be called “Shapeshifts Natural Form” because you need your own version that has a few different effects to the standard one. You might want to make 10 of these for example, for each shapeshift spell you have. You do not want 10 extra entries in dialog.tlk all saying the same thing. Instead you can hex-edit the files to all point at the one existing string that says what you want.
In BG2 this string is at reference 11826. This is 0x2E32. So you would go to offset 0x8 and the IEFFHP website will also tell you that this field is 4 bytes long. You would type in 32 2E 00 00 because it is in little-endian format and is 4 bytes (32 bits) long. If you now load up the spell in IEEP, the spell name should be Shapeshifts Natural Form.
Links and contact information
You will find very helpful data at the Infinity Engine File Format Hacking Project website: http://www.ugcs.caltech.edu/~jedwin/baldur.html#FileFormats .
These pages show you all the known values in the known file types, listed in order of hex offset.
This guide was meant as an introduction to hex-editing and not as an exhaustive how-to. If you have any further questions, or notice any errors in this document, please email me, the author at vaskez@runbox.com. You can also leave a message in my guest book on my site http://vaskez.tripod.com if you just want to comment generally, or give suggestions as to how this guide can be improved. Then others will see your idea and it will not get repeated again and again.
Vaskéz